Exercício da intersecção entre duas equações de 2º grau

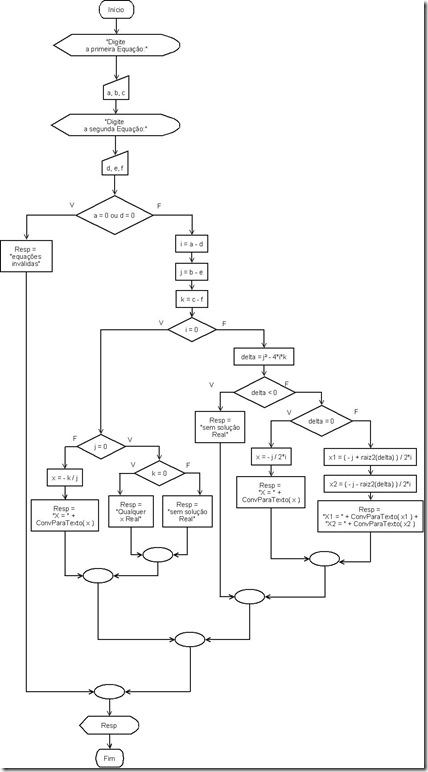
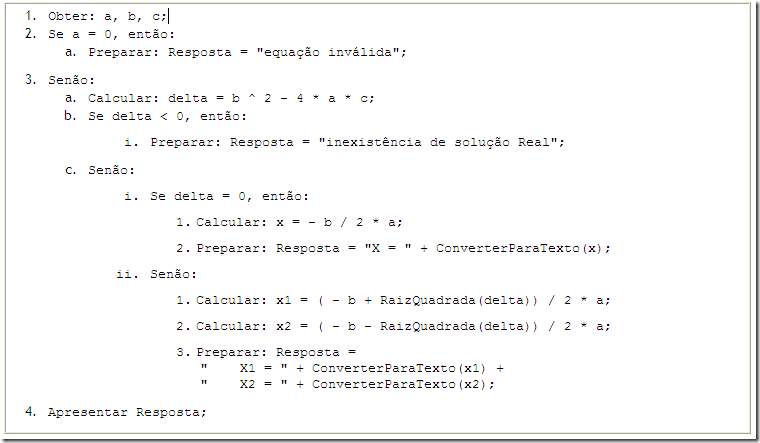
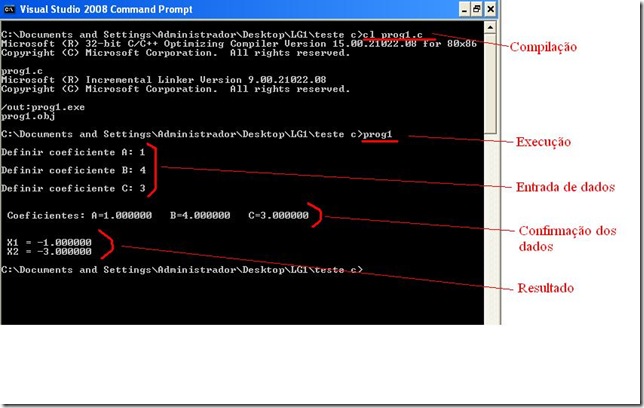
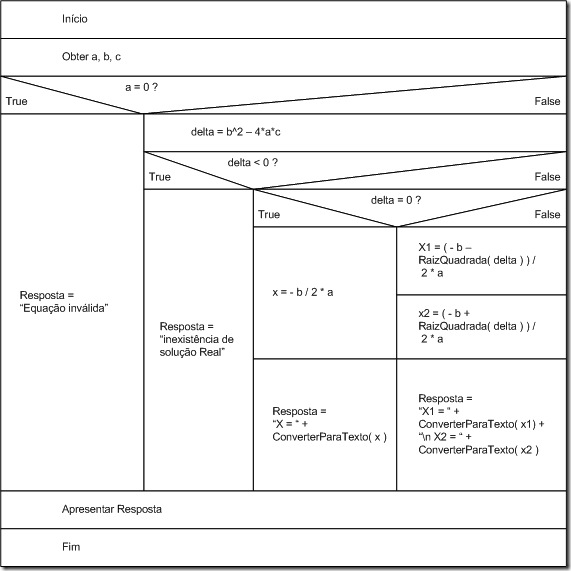
Diagrama de blocos construído com o software DIA:

 

A ferramenta de apoio DIA pode ser obtida em:

http://downloads.sourceforge.net/dia-installer/dia-setup-0.96.1-8.exe

 

 

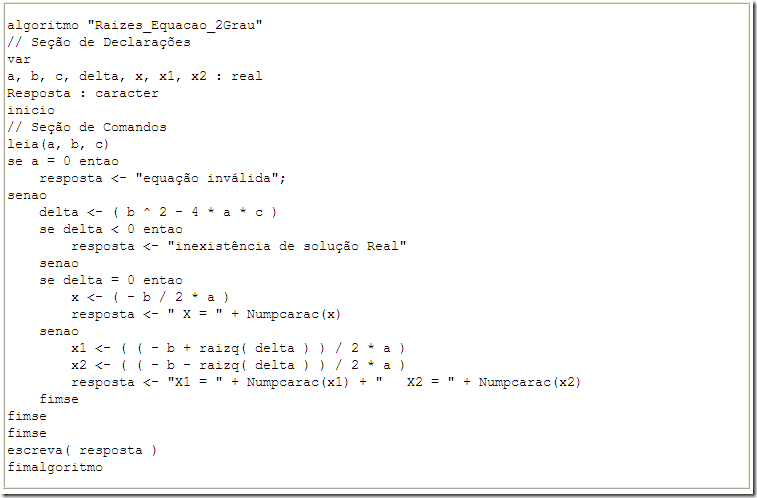
A seguir temos o algoritmo escrito em "portugol" nativo do software VISUALG:

 

algoritmo "intersecção"
// Função :
// Autor :
// Data : 29/08/2008
// Seção de Declarações
var
a, b, c, d, eh, f, i, j, k, delta, x, x1, x2 : real
Resp : caracter

inicio
// Seção de Comandos
escreva("Digite a primeira equação:")
leia(a, b, c)
escreva("Digite a segunda equação:")
leia(d, eh, f)
se ( a = 0 ) ou ( d = 0 ) entao
   Resp <- "Equações inválidas"
senao
   i <- ( a - d )
   j <- ( b - eh )
   k <- ( c - f )
   se ( i = 0 ) entao 
      se ( j = 0 ) entao
         se ( k = 0 ) entao
            Resp <- "Qualquer x Real"
         senao
            Resp <- "sem solução Real"
         fimse
      senao
         x <- ( - k / j )
         Resp <- "X = " + Numpcarac( x ) 
      fimse
   senao
      delta <- ( j ^2 - 4 * i * k )
      se ( delta < 0 ) entao
         Resp <- "sem solução Real"
      senao
         se ( delta = 0 ) entao
            x <- ( -j / 2 * i )
            Resp <- "X = " + Numpcarac( x )
         senao
            x1 <- ( ( -j + raizq( delta ) ) / 2 * i )
            x2 <- ( ( -j - raizq( delta ) ) / 2 * i )
            Resp <- "X1 = " + Numpcarac( x1 ) + "   X2 = " + Numpcarac( x2 )
         fimse
      fimse
   fimse
fimse
escreva( Resp )
fimalgoritmo

 

 

VisuAlg pode ser obtido em:
http://www.apoioinformatica.inf.br/

E seu manual em:

http://hermes.ucs.br/carvi/cent/dpei/haklauck/algoritmos/Linguagem_Visualg2.0.pdf

 

Bom estudo e até a próxima.

Linguagem C - variáveis tipo "int"

 

Vejam teste utilizando Microsoft Visual Studio 2008 C++ 9.0 para demonstrar o tamanho em bytes alocados para cada variação de uso do tipo "int":

É isso aí.

Até a próxima.

Reescrevendo o algoritmo para resolver o problema da equação 2º grau

Utilizando um editor de textos, como o Microsoft Word, Open Office ou mesmo o Notepad, facilmente podemos organizar os passos que constituem a lógica para resolver o problema apresentado:

 

Podemos encontrar sintaxes variadas para o pseudo-código, também largamente difundido como "Português Estruturado", até mesmo com forte influência da linguagem de programação Pascal. Nessa linha de abordagem, a sintaxe praticamente constitui uma versão da linguagem Pascal traduzida para a língua portuguesa. A título de exemplo, o algoritmo acima poderia ter o seguinte aspecto:

 

Links de interesse:

• VisuAlg
  http://hermes.ucs.br/carvi/cent/dpei/haklauck/algoritmos/Linguagem_Visualg2.0.pdf
  http://www.apoioinformatica.inf.br/
• Notepad++
  http://notepad-plus.sourceforge.net/uk/download.php

Pretendo direcionar o esforço que seria dispendido para aprender e dominar a "linguagem PASCAL VisuAlg", para um melhor aprimoramento, fixação e desenvolvimento na linguagem de programação C/C++ e testar os algoritmos diretamente numa plataforma realista, como por exemplo os compiladores Embarcadero(ex-CodeGear(ex-Borland)) C/C++ Builder, Microsoft C++ DotNet e GNU/Linux GCC.

 

 

Bom estudo e até a próxima.

Implementando a solução na Linguagem de Programação C

 

O código a seguir foi elaborado com base nas soluções apresentadas anteriormente em Diagrama de Blocos e NS (Nassi-Schneiderman):

 

#include <stdio.h>
#include <math.h>

void main()
{
    char Resposta[50];

    float a, b, c, delta, x1, x2, x;

    printf( "\nDefinir coeficiente A: " );
    scanf( "%f", &a );

    printf( "\nDefinir coeficiente B: " );
    scanf( "%f", &b );

    printf( "\nDefinir coeficiente C: " );
    scanf( "%f", &c );

    printf( "\n\n Coeficientes: A=%f   B=%f   C=%f \n\n", a, b, c );

    if ( a == 0 )
    {
        sprintf( Resposta, "\n Equacao invalida \n" );
    }
    else
    {
        delta = pow( b, 2 ) - 4 * a * c;

        if ( delta < 0 )
        {
            sprintf( Resposta, "\n Nao possui solucao Real \n" );
        }
        else
        {
            if ( delta == 0 )
            {
                x = - b / 2 * a;
                sprintf( Resposta, "\n X = %f \n", x );
            }
            else
            {
                x1 = ( - b + sqrt( delta ) ) / 2 * a;
                x2 = ( - b - sqrt( delta ) ) / 2 * a;
                sprintf( Resposta, "\n X1 = %f \n X2 = %f \n", x1, x2 );
            }
        }
    }

    printf( "%s", Resposta );

}

 

Na solução foram utilizadas as seguintes funções da biblioteca <stdio.h>:

• printf( )
• scanf( )
• sprintf( )

E da biblioteca <math.h>:

• pow( )
• sqrt( )

A seguir temos a cópia da tela "prompt de comandos" do sistema Windows XP, onde podemos observar as etapas de compilação e execução do programa:

 

A Microsoft distribui gratuitamente a versão Microsoft Visual C++ 2008 Express Edition:

http://www.microsoft.com/Express/

 

 

Até a próxima.

Uso do Diagrama de Nassi-Schneiderman

A solução para o mesmo problema, agora com o uso do diagrama Nassi-Schneiderman:

 

 

Este diagrama também é chamado de Diagrama de Chapin.

Referências:

• "Nassi-Shneiderman Charts: An alternative to Flowcharts for Design.":
  http://www.cs.umd.edu/hcil/members/bshneiderman/nsd/Yoder-Schrag-nassi_schart.pdf
• Isaac Nassi:
  http://www.nassi.com/ike.html
  http://en.wikipedia.org/wiki/Isaac_Nassi
• Ben Schneiderman:
  http://www.cs.umd.edu/~ben/ 
  http://en.wikipedia.org/wiki/Ben_Shneiderman
• Ned Chapin: 
  http://www.almexperts.com/ExpertWitness/experts_and_consultants/expert/5160968.html

 

Até a próxima.

Uso do Diagrama de Blocos

Para resolver o problema proposto, a seguir temos a seqüência lógica dos procedimentos necessários apresentada através do recurso Diagrama de Blocos:

 

 

Links indicados para leitura complementar:

http://www.manzano.pro.br/tutor/algoritmo/ptalg006.zip

http://www.fw.uri.br/~leticia/ApostilaAlgoritmos2006.pdf

 

Até a próxima.

Uma abordagem para a resolução das raízes de uma equação de 2º grau

Algoritmo expresso em forma textual de uma seqüência imperativa de comandos:

1) Obter coeficientes a, b, c;
2) Coeficiente a = 0 ?
    2.1) Então: preparar Resposta = "equação inválida";
    2.2) Senão:
        2.2.1) Calcular delta = b^2 - 4*a*c;
        2.2.2) Valor de delta < 0 ?
            2.2.2.1) Então: preparar Resposta = "inexistência de solução Real";
            2.2.2.2) Senão: valor de delta = 0 ?
                2.2.2.2.1) Então:
                    2.2.2.2.1.1) Calcular x = - b / 2 * a;
                    2.2.2.2.1.2) Preparar Resposta = "X = " + ConverterParaTexto( x );
                2.2.2.2.2) Senão:
                    2.2.2.2.2.1) Calcular x1 = ( - b + RaizQuadrada( delta ) ) / 2 * a;
                    2.2.2.2.2.2) Calcular x2 = ( - b - RaizQuadrada( delta ) ) / 2 * a;
                    2.2.2.2.2.3) Preparar Resposta = "    X1 = " +
                                                        ConverterParaTexto( x1 ) + 
                                                    "    X2 = " +
                                                        ConverterParaTexto( x2 );
3) Apresentar Resposta;

 

Considerações:

1) o conceito de biblioteca de funções, previamente implementadas na maioria das linguagens de programação de alto nível, permite a abstração de certas operações elementares e corriqueiras, como exemplo a linguagem de programação C Ansi oferece:

• obtenção de raiz quadrada:  sqrt( valor );
• conversão/concatenação de dados diversos para texto: sprintf( buffer, "formatação", variáveis );

2) as operações aritméticas básicas são normalmente representadas pelos símbolos: + - * /

3) o operador de exponenciação ou potenciação vai depender da linguagem de programação: ** ou ^ são os casos mais usuais, porém tomando a linguagem de programação C Ansi como exemplo, existe a função de biblioteca pow(a, n) para calcular a elevado a n;

4) também é comum a necessidade de concatenção de textos, variando muito entre as linguagens de programação, mas podendo ser representada pelo operador + ou & ou até mesmo por funções de biblioteca; no caso da linguagem C Ansi podemos usar a mesma função sprintf() mencionada acima;

5) ao fazer uso de operadores relacionais >, < e = devemos tomar cuidado para não confundir o teste de igualdade com a operação de atribuição:

Atribuição	Teste de igualdade	Linguagem
delta = pow(b,2) - 4 * a * c	if ( delta == 0 )	C ansi, C++
delta := b ** 2 - 4 * a * c	if ( delta = 0 )	Pascal, Delphi

6) por último, uma consulta ao dicionário Michaelis (http://michaelis.uol.com.br/moderno/portugues/index.php?lingua=portugues-portugues&palavra=dentear) nos apresenta o verbo: "dentear (den.te.ar) (dente+ear) vtd 1 Formar dentes em. 2 Recortar, chanfrar. Var: dentelar.". Reparar que o algoritmo acima apresentado em forma textual, assim como a escrita de comandos na maioria das linguagens de programação de alto nível, devem usar este recurso para facilitar a leitura dinâmica dos mesmos e agilizar a compreensão do raciocínio, assim como acelerar e manter um controle sobre o fluxo de execução das instruções; ou seja, um hábito a ser desenvolvido.

 

Até a próxima.

 

Propondo um problema clássico para estudo

Dada uma equação de 2º grau genérica:

Encontrar a solução para f(x) = 0, obedecendo a restrição do domínio dos números Reais.

Os coeficientes a, b, c deverão ser informados como entrada para o algoritmo a ser desenvolvido.

Utilizar o método de Bhaskara (http://pt.wikipedia.org/wiki/Bhaskara) e como resposta considerar as possibilidades:

1) equação inválida;

2) inexistência de solução Real;

3) uma raiz apenas;

4) duas raízes;

 

Até a próxima.

LG1 - Segundo semestre de 2008

 

Boas-vindas para todos e expresso aqui meus votos para que tenham um proveitoso semestre.

Um grande abraço e até a próxima.